As part of the Canadian Distributed Mentorship Program, here is where I will be posting my journal entries relating to the work done.

I -

II -

III -

IV -

V -

VI -

VII -

VIII -

IX-

X-

XI-

XII-

XIII-

XIV-

XV-

XVI-

XVII-

XVIII

What I didn't mention in the last entry was that I have taken a break from the Nortel project. In between two bisimulation lectures, over a batch of shortbread cookies, Doina and I were talking about my new found love for Predictive State Representations. She suggested that I should start reading the current literature available, as it might come useful in the future. Chris Hundt, a former McGill student, has a lovely summary page of what the interweb has to offer. Half a dozen papers and 4 small trees later, with plans of world domination disguised as a grocery shopping list, I had jumped on the PSR bandwagon. It's a very different bandwagon than the one I usually hang out on. Since about three weeks ago I cashed the "Get out of explaining PSR's in detail for free" card, I think I ought to do this now. Buckle your seat belt Dorothy, because POMDP's are going bye-bye.

Reinforcement learning is all about setting your agent loose in an environment, and allowing her to learn from the actions performed. Every action is rewarded according to a reward function, (rewards are loosely defined here...a penalty, i.e. a reward of -1 is still a valid reward), and the agent tries to maximize the total reward. The challenge comes when you have a vague idea of what your optimal policy is, but haven't explored the entire environment...do you perform the qvasi-optimal action and get the best score you think you could get, or do you take a knowingly bad action to explore the environment and maybe get that really optimal policy? Dum dum dum.

That, alas, is a decidedly naive view of the world. It assumes lovely things, such as the fact that the environment provides you with perfect state information, and that you have a pre-defined idea of the system dynamics (transition probabilities from one state to another). It is the unfortunate reality that a robot, who I will name Montserrat so I can talk about him in more formal manners, has no such information. Montserrat doesn't really know in what room he is roaming about, has a faulty left eye sensor, doesn't know his name is Montserrat, and of late has become rather senile and can't store as much data as he once could, back in the good old days. Your first approach is now rendered useless: the faulty sensor gives you innacurate state information (when you think you are is positively not where you are. Or it might be, but it doesn't really matter, as you can't tell anyway), you don't have the memory to try to save all the data about the environment, and noone has given you the state transition probability distributions. If I were Montserrat, I would eat a lampshade and call it quits. But, there is no need for such furniture profanities, as we have...PSR's.

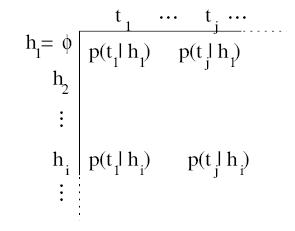
The time is now to introduce the Float-Reset problem: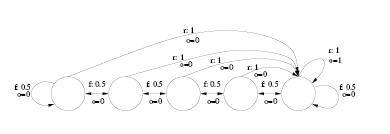

A float action moves, with a probability of 0.5 to an adjacent state, including itself, and always returns an observation of 0. A reset action returns to the initial state (farthest right), and returns an observation of 1 only if the state where the reset action was performed was the initial state.

Note: the following explanation is summarized from Michael James' paper. I'm going to ignore the problem of learning optimal policies for now, as they're a bit of a blur. Rather, we're going to look at learning the environment. Ideally, given a history and a future, you would like to know the probability of seeing that future. One tries to achieve this by constructing, updating, watering and extracting core tests from a System Dynamics Matrix. The idea is that the system can be viewed as a probability distribution over all possible futures of all lengths. So, we're going to need two things: a test, which is an action:observation sequence, i.e. t = [a_0:o_0, a_1:o_1...], and represents a prediction, and a history, which is a test starting at the beginning of time, that has already happened. The System Dynamics matrix will be constructed as follows: the rows correspond to all possible histories, while the colums represent all possible tests. An entry (i,j) is the probability of the future i given past j:

So now we've learned what are the chances of seeing some future given that we've seen a past. Which is a fairly nice thing to know. We're nowhere near the end of this explanation, but I think the dork rating of this entry is through the roof already, and the main ideas have been thrown around enough, so I'll talk about core tests et. al next week...

On an even dorkier side of the cube, the World Cup is on, and as such, I've lost my mind. Because I lose about 3 hours watching 22 men kick a football around, my lab hours have shifted dramatically. I haven't left the lab before 11 in so long that my roomate doesn't remember what I look like. Rest assured, I live him funny notes around the house, and produce as many dirty dishes as before, to make out for my absence. I'm sure he appreciates it. :)